Again consider the differential equation
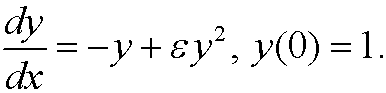
As we said before, the exact solution is then
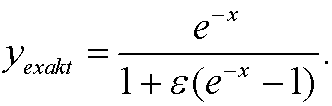
By using maclaurin expansion we know that
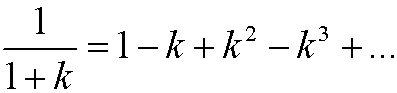
for small values of k. If we insert
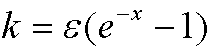
we get
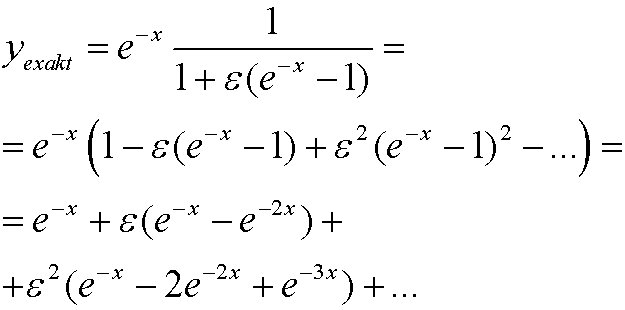
Now compare with the approximate solution from last part
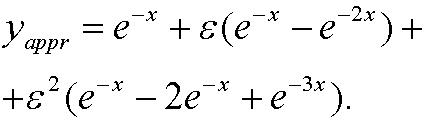
We see that the error E in the approximation thus is
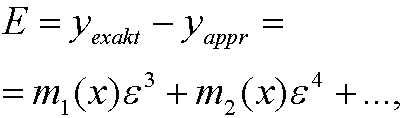
for some dunctions m1(x), m2(x),… (that we can compute!). We say that the error E is of order ![]() and write E=O(
and write E=O(![]() ), where O stands for big ordo.
), where O stands for big ordo.