Consider a mass m that is suspended in a spring, where the restoring force F is supposed to be
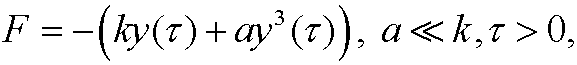
in the distance y from the equilibrium point (with minus sign because the force is opposed to the direction of motion). Newton’s second law then gives
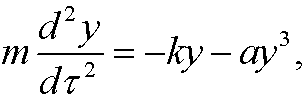
with the initial conditions (the mass is dropped from a positive displacement A)
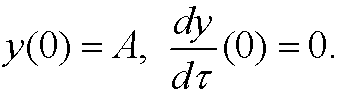
We rescale this problem according to
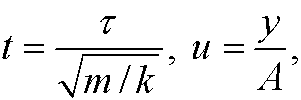
(see chapter 1) and get the equation
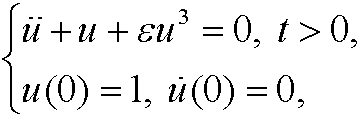
where
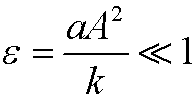
is a dimensionless parameter. This is Duffing’s equation. We try to solve it with our perturbation method. Insert
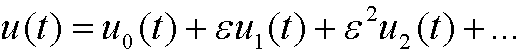
in the rescaled differential equation:
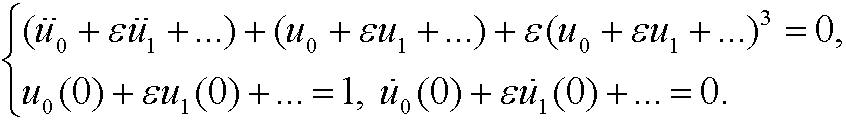
Now compare powers of ![]() :
:
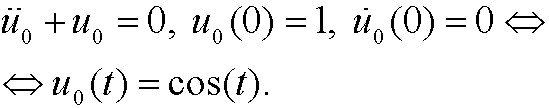 |
|
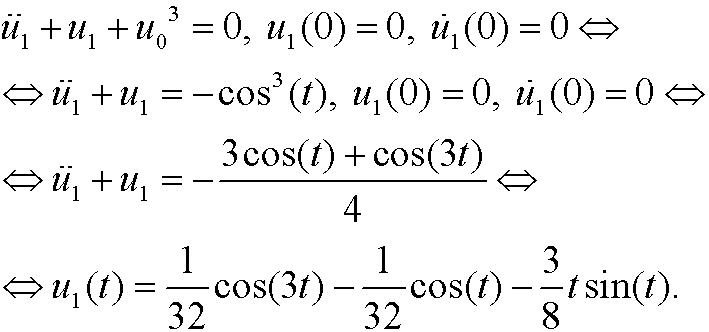 |
An approximate solution is thus
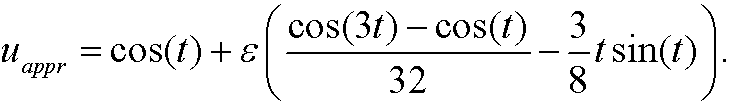
Note that:
(i) the leading term cos(t) seems correct.
(ii) if t<=T0 and ![]() is “small” then the correction term is “small”.
is “small” then the correction term is “small”.
(iii) if we let t to be large (![]() ) , the correction term can be large even though
) , the correction term can be large even though![]() is small.
is small.
Remark: The problem in (iii) is due to the secular term
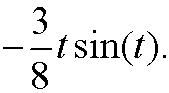
Our next move will be to introduce a method that avoids this problem.