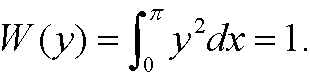7.1) Consider the functional
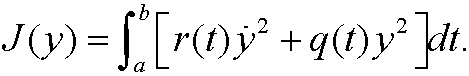
Find the Hamiltonian H(t,y,p) and state the canonical equations for the problem.
7.2) Derive Hamilton’s equations for the functional
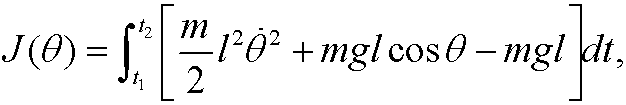
representing the motion of a pendulum in the plane.
7.3) Consider a system of n particles where mi is the mass of the i:th particle and (xi,yi,zi) its position in space. The kinetic energy of the system is
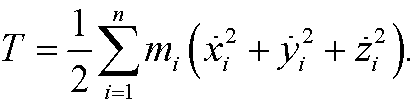
Assume that the system has potential energy
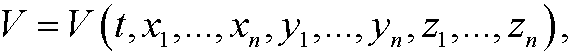
so that the force acting on the i:th particle has the components
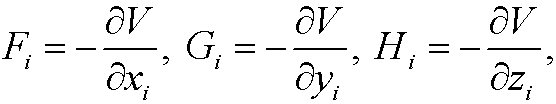
in the x-, y- and z-directions. Show that Hamilton’s principle imply the equations
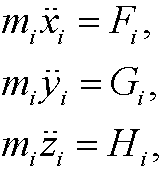
Newton’s equations for a system of n particles.
7.4) The American post office prescribes that the sum of the length a and the circumference p=2b+2c of a cross section of a box may not exceed 100 inches.
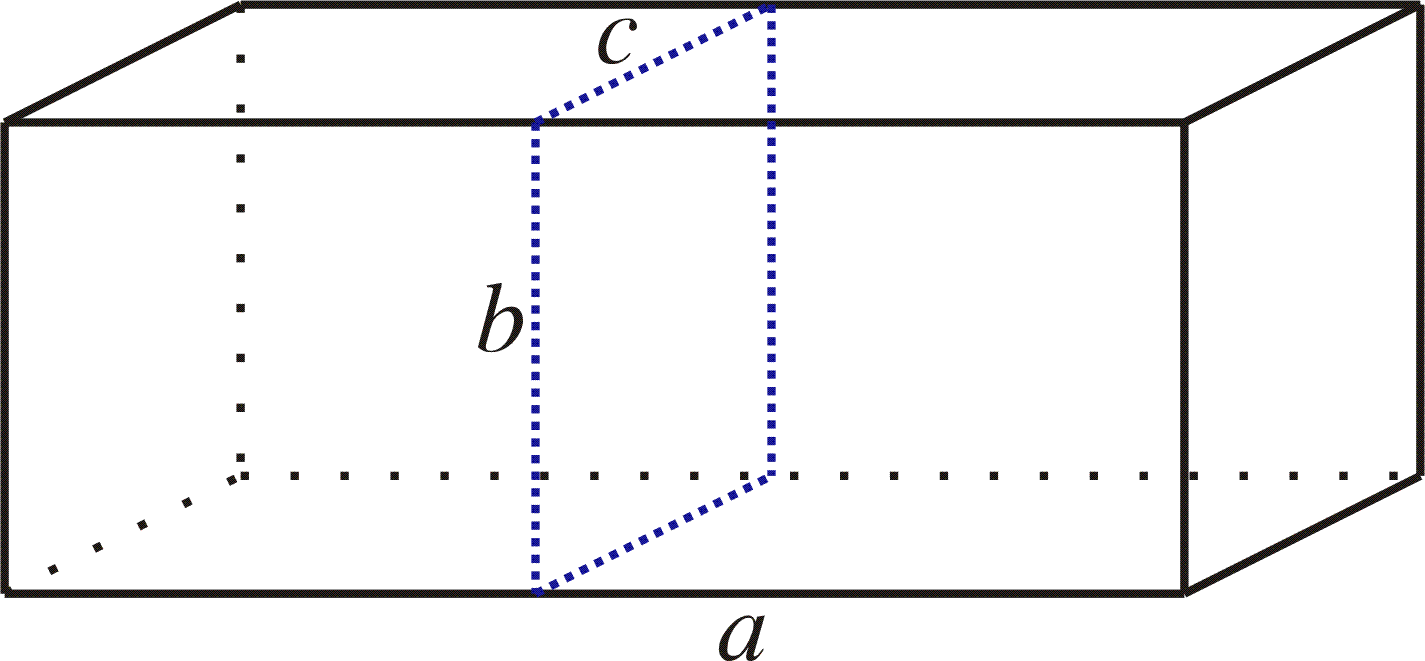
Find the proportions of the allowed box with maximal volume.
7.5) Compute the shortest distance d from a point on the ellipse x2+4y2=4to the line x+y=4.
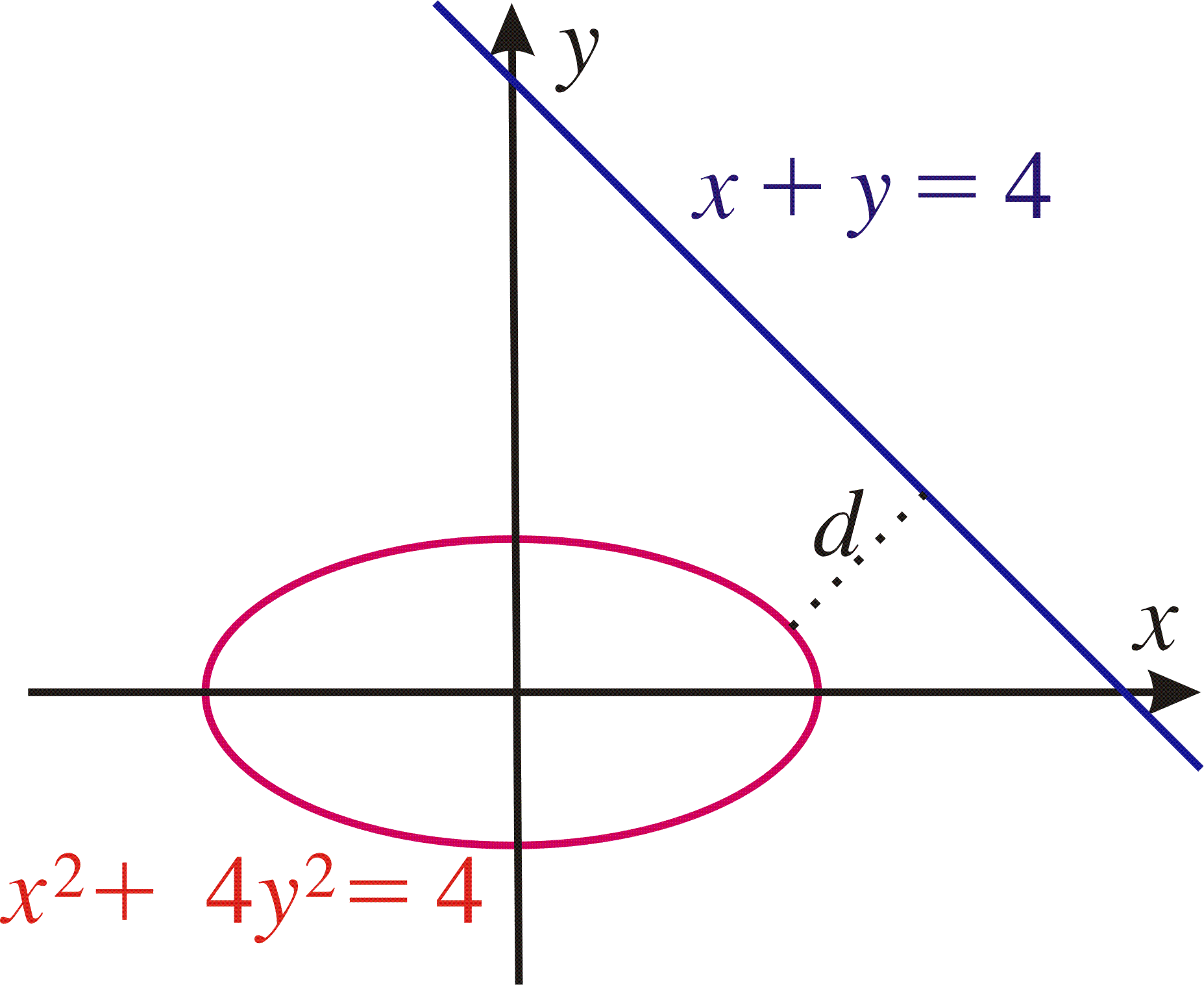
7.6) Find the extremals to the isoperimetric problem
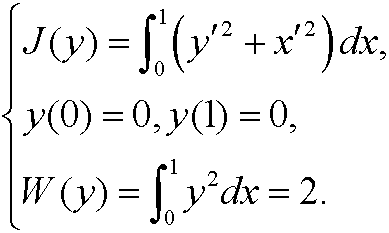
7.7) Determine the equation for the shortest curve in the first quadrant that passes through the points (0,0) and (1,0) and that together with the x-axis encloses a give area A, where
![]()
7.8) Find the extremals to the isoperimetric problem
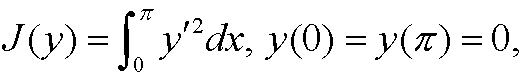
under the constraint