We rescale the problem by putting
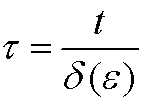
in our original differential equation
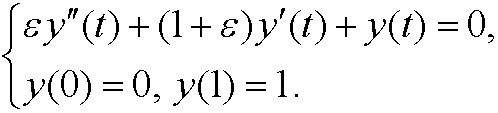
If
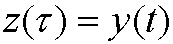
we get
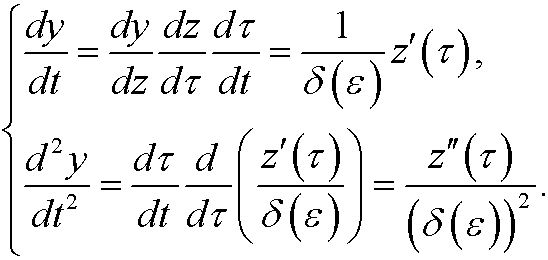
The equation then transforms to
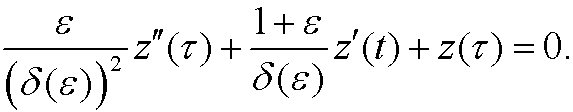
Consider the coefficients
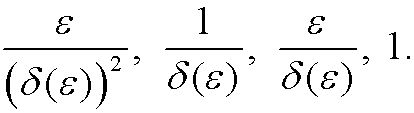
The problem in the original equation is that the coefficient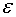 
of the highest derivative y” is small compared to the others. To avoid this problem we thus choose the main coefficient
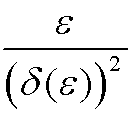
to be of the same order as one of the other coefficients and that the other two coefficients are comparably small. We demonstrate the procedure below (remember that is small):
| Case 1): |  |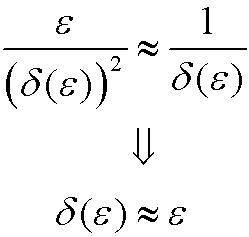
 |
 |
|
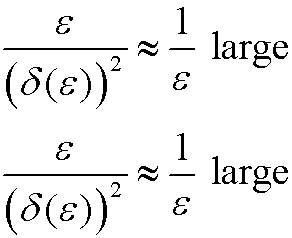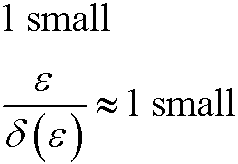Case 2): |
 |
 |
 |
|
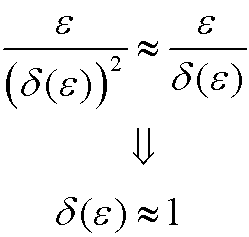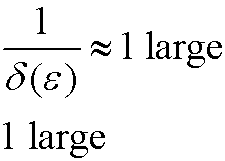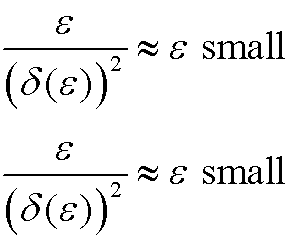Case 3): |
 |
 |
 |
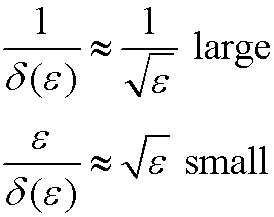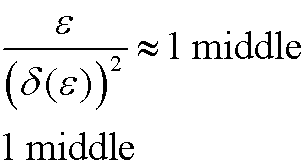Ve see that we only have one possibility and that is Case 1, where the main coefficient is relatively larger than the remaining coefficients. We therefore choose
Our transformed equation then becomes
If we now put 
we get the equation
with the solution
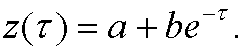
The boundary condition z(0)=y(0)=0 then yields that
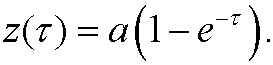
Our inner approximation is thus
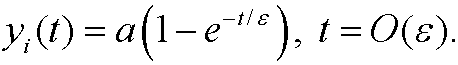
The remaining problem is thus to determine the constant a and match the inner and outer approximations.