Poincaré-Lindstedt’s method is a method to avoid secular terms. Vi introducerar en “störd” tid
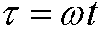
where
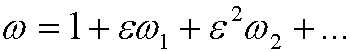
and put
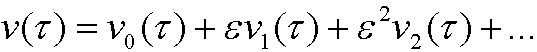
Example: We examine Duffing’s equation
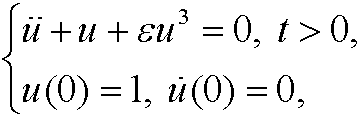
again. By doing the change of variables
the equation is transformed to
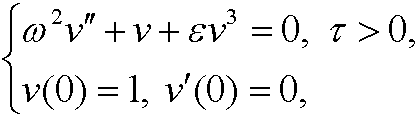
since
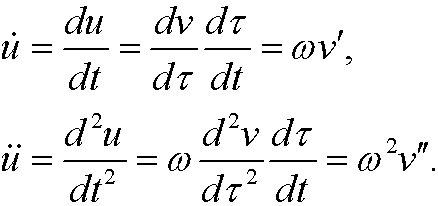
If we insert the the expressions for ![]() and u in this we get
and u in this we get
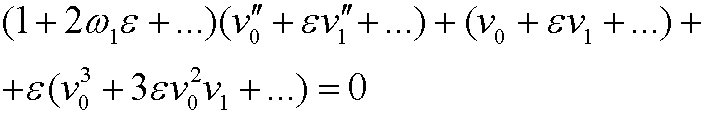
and
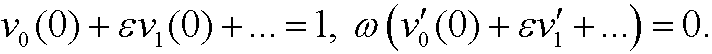
Now we compare powers of ![]() :
:
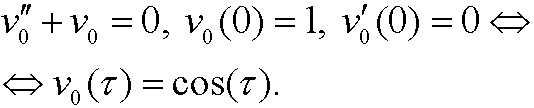 |
|
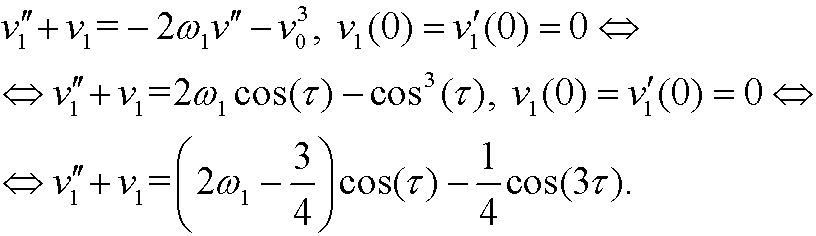 |
By choosing
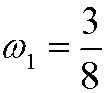
we see that we can avoid the secular term. This leads to
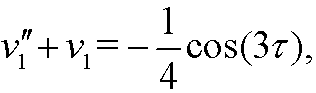
with the solution
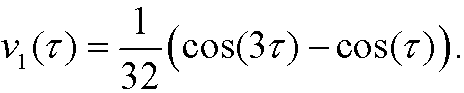
Alltogether we have that a first order perturbation solution of Duffings equation is
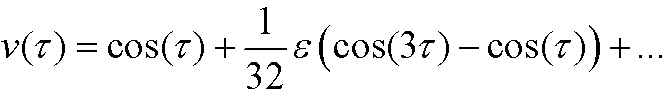
where
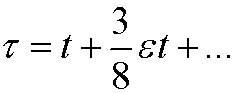
Remark: Poincaré-Lindstedt’s method works for some (not all) equations on the form
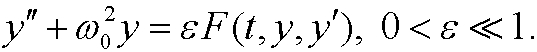
Troubles arise when also the right hand side has the frequency ![]() in some step. We will then not succeed with the particular solution
in some step. We will then not succeed with the particular solution
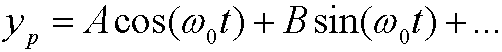
but instead have to try with
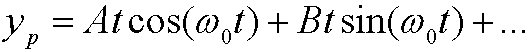
which leads to secular terms. This trouble can be avoided in Poincaré-Lindstedt’s method by instead put
and then solve the corresponding equations as usual.