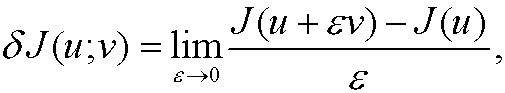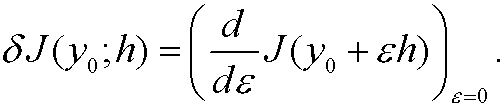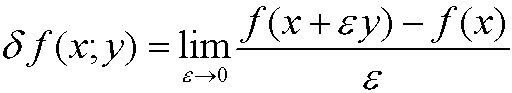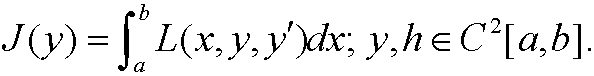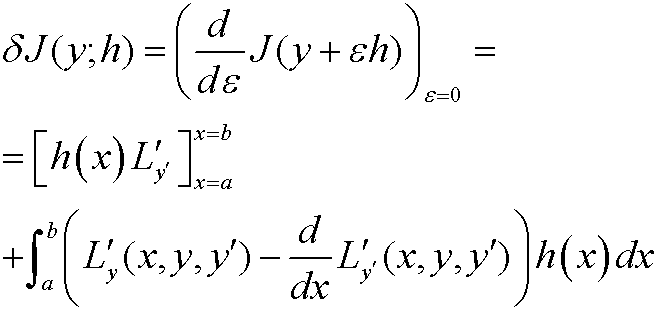13. Differentiation of functionals.
If u and v are elements in the vector space X we define the Gâteau-variation of the functional J(u) in the direction v according to
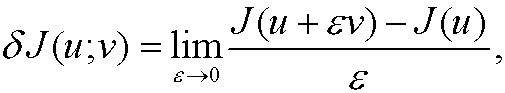supposed that this limit exists.
Remark: This means that
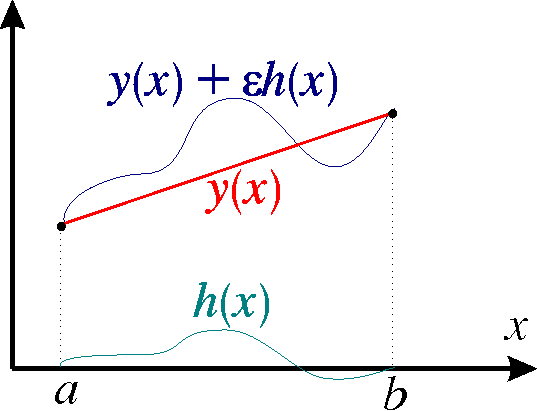
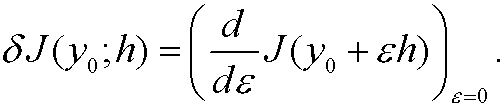The increment eh is called the variation of the function y0.
Exampel 23: Suppose that J in this case is a real valued function f in C1[a,b] defined for x in Rn. If y is a unit vector in Rn then
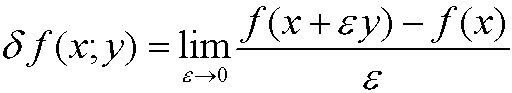the direction derivative to f in the direction y. By making a taylorexpansion we see that
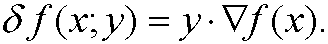Example 24: (Compare theorem 1 and the proof in part 8). Consider the functional
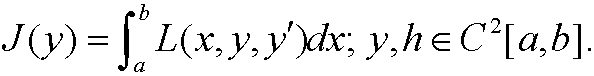Then
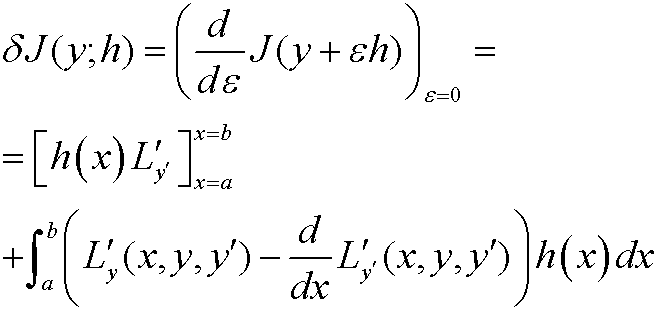Geometrical interpretation of competing curves:
