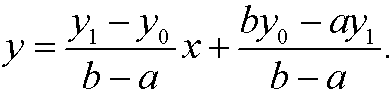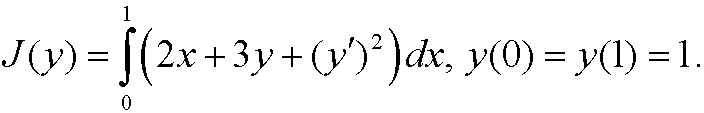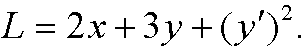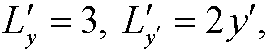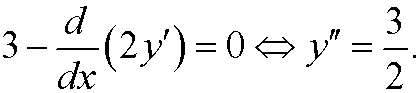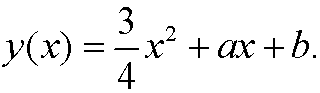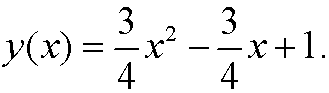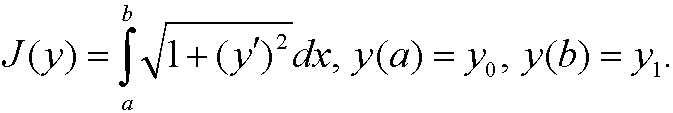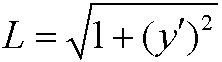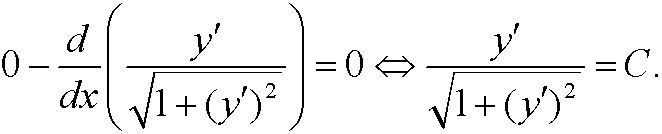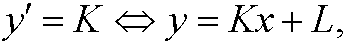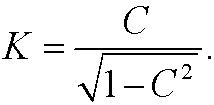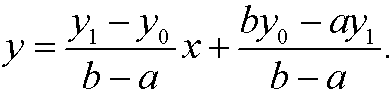6. Two solved problems.

Example 10: Find the extremal to the functional

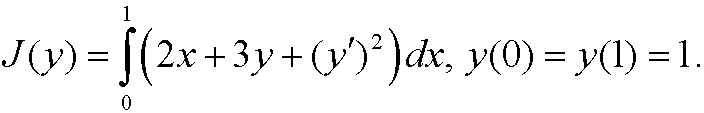Solution: Here we have

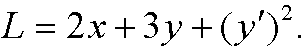This implies that

and Euler’s equation therefore becomes

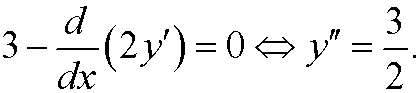Two integrations give

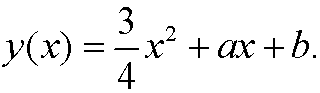With the boun dary conditions inserted the solution becomes

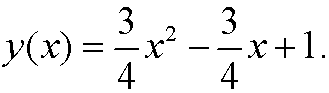
<>Example 11: (Compare example 4.) Find the extremal to the functional

Solution: The lagrangian is

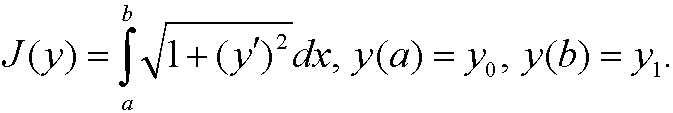
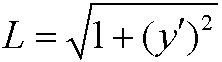and Euler’s equation thus becomes

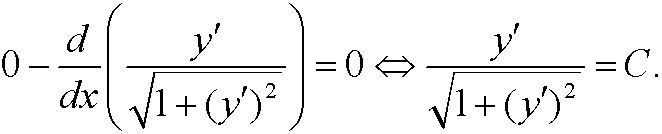If we solve fory‘ we get

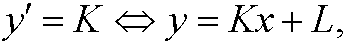where

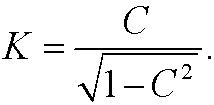With the boundary conditions inserted we then get