9.1) Draw the phase portrait for the system
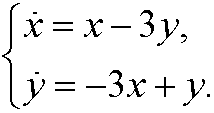
9.2) Draw the phase portrait for the system
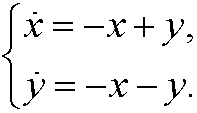
9.3) Find the general solution and draw the phase portrait for the system
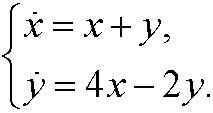
9.4) Draw the phase portrait for the system
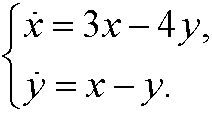
9.5) The equation for a damped harmonic oscillator is
Rewrite the equation as a system by introducing the variable
Show that (0,0) is a critical point. Describe the properties and stability of the critical point in the cases:
a) a=0,
b) a2-4km=0,
c) a2-4km<0,
d) a2-4km>0.
9.6) Describe Verhulst’s population model. In particular describe how this model can be used to illustrate the notions of attractor and chaos. What is Feigenbaum‘s constant?
9.7) Describe how to illustrate Julia sets. What is the famous Mandelbrot set?