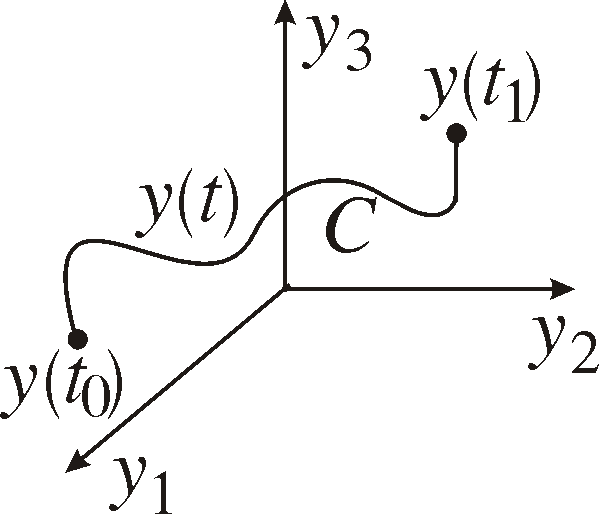
We will in this chapter use calculus of variations to get the equations of motion for a mechanical system. I next part we will see that the motion of the system is such that a specific integral is minimized. Consider a mechanical system
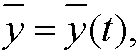
that is
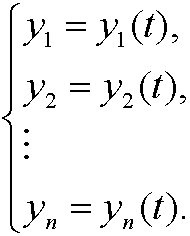
Here
are the so called generalized coordinates and
are called generalized velocities. If aij are known functions of the coordinates y1,y2,…,yn, we denote
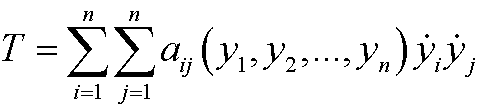
the generalized kinetic energy and the generalized potential energy as
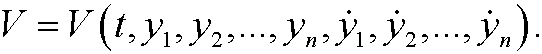
We can now define the Lagrangian as
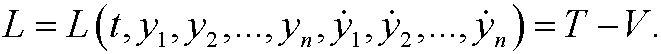
If we consider the general coordinates y1,y2,…,yn, as coordinates in Rn the equations
can be considered parametric equationes for a curve C connecting two states S0 and S1 in space.