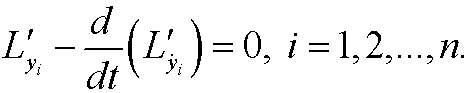6. The general case.

We define the n canonical momentums 

 

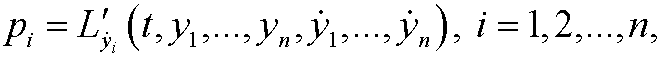
for the general action integral

 

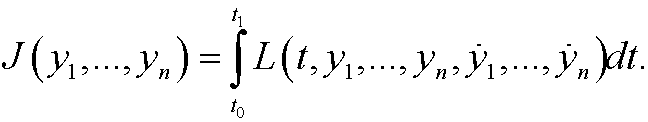
If we assume that

 

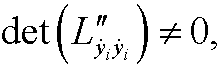
we can via the implicit function theorem solve the system of momentums for the variables

 

and get

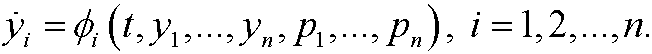
We now define the Hamiltonian by

 

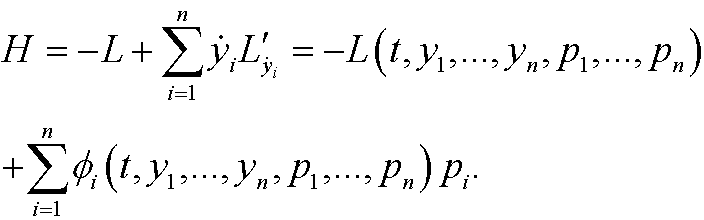
By using similar arguments as in the previous part we get Hamilton’s equations:

 

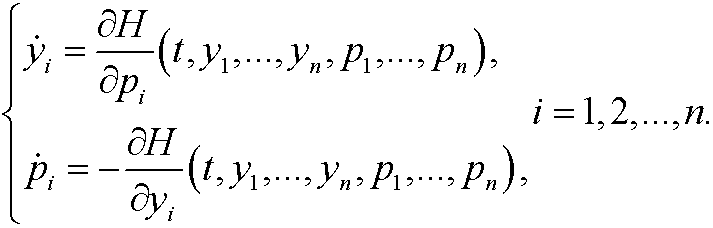
This is a system of 2n first order ordinary differential equations in the unknown funktions y₁,y₂,…,y_n, and the unknown momentums p₁,p₂,…,p_n. The system contains the same information as the corresponding n second order Euler-Lagrange’s equations