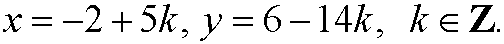A diophantine equation is an equation where only integer solutions are accepted. This implies that diophantine equations becomes harder (or even impossible) to solve than equations that do not have this restriction. We will show that diophantine equations of the type
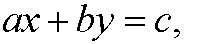
a, b ,c, x, y integean be solved by Euclid’s algorithm (assuming that there is a solution). The method of solution depends of the coefficients a, b and c. We have three different variants that we treat in the examples below:
Example 1: Solve the equation
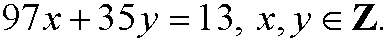
First we examine gcd(97,35). We have
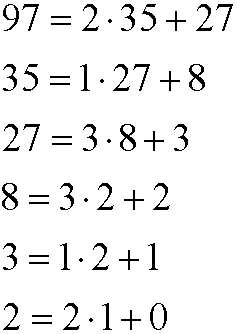
This means that gcd(97,35)=1. Now we go backwards and express gcd(97,35) as a linear combination of 97 and 35:
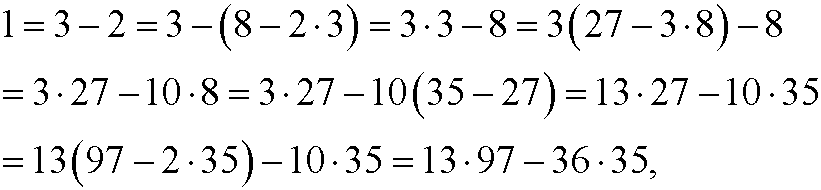
that is
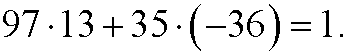
If we multiply this equation by 13 we get
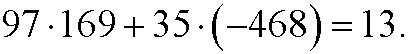
which means that one solution of the diophantine equation is x=169, y=-468. This is however not the only solution. We can exactly as in part 3add and subtract the least common multiple
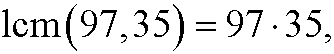
such that
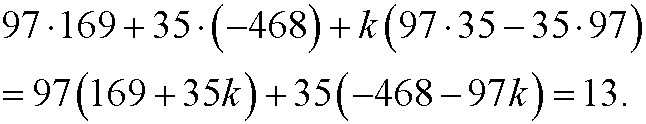
We thus have infinitely many solutions
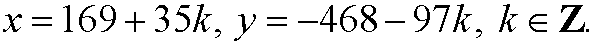
Example 2: Solve the equation
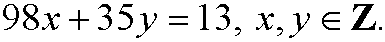
First we examine gcd(98,35). We have
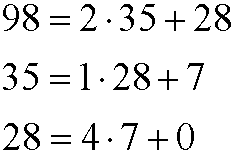
This implies that gcd(98,35)=7, which means that every linear combination of 98 and 35 must contain the factor 7. Then also 98x+35ymust be a multiple of 7. But since the right hand side 13 does not contain the factor 7, there are no integer solutions to this equation.
Example 3: Solve the equation
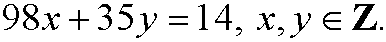
We had from example 2 that gcd(98,35)=7. If we go backwards and express gcd(98,35) as a linear combination of 98 and 35 we get:
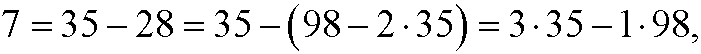
that is
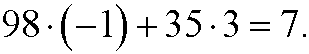
If we multiply this equation by 2 we get
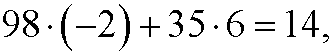
which implies that one solution to the diophantine equation is x=-2, y=-6. This is however not the only solution. We can exactly as in part 3 add and subtract the least common multiple
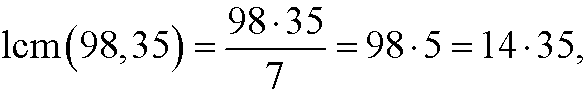
such that
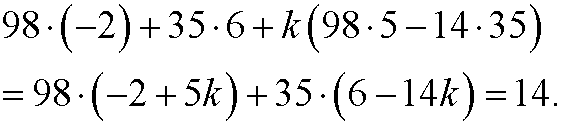
We thus have infinitely many solutions