Proof by induction is a method of proving (countably) infinitely many propositions at a time. A proof by induction consists of a basis step and an induction step. In the basis step one proves the proposition for the simplest possible case. Then one proves that if the proposition holds for a specific case, then this implies that the proposition also holds for the next case. We can illustrate the procedure as an infinite line of domino bricks; the basis step corresponds to falling the first domino brick while the induction step corresponds to that if one brick falls, the next will also fall. It is not hard to realize that we in this case will fall all bricks by falling the first.
Axiom of induction: Let Pn be a proposition depending on the integer n. If
1) Basis step: P1 is true (proposition is true for n=1)
2) Induction steg: Pp implies Pp+1, that is, if the proposition is true for n=p then it must also be true for n=p+1
then the proposition is true for all integers n=1,2,3,…
Example 1: We note that 61=6, 62=36, 63=216, 64=1296, that is, the first 4 integer powers of 6 has the last digit 6. Let us show that this true for all positive integer powers 6n.
Basis step: 61=6 has last digit 6.
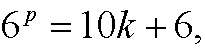
for some integer k. If this assumption holds, we have for 6p+1 that
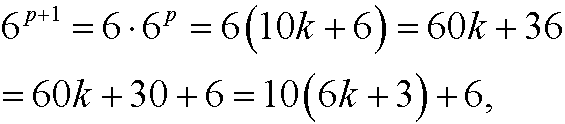
that is, 6p+1 also has last digit 6.
Since we have shown that the proposition holds for the basis step n=1 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=1,2,3,…
Example 2: Show that
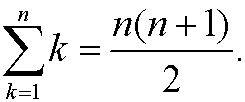
Basis step: We have that
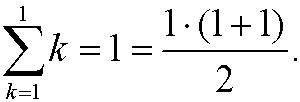
Induction step: We assume that the formula is correct for n=p, that is
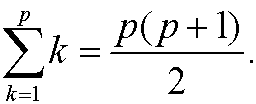
We want to show that it then also must hold that
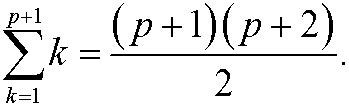
We have that
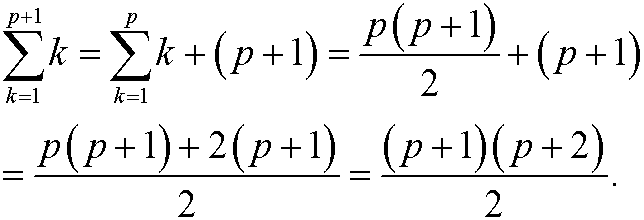
Since we have shown that the proposition holds for the basis step n=1 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=1,2,3,…
Example 3: Show that
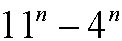
is divisible by 7 for every n=1,2,3,…
Basis step: We have that
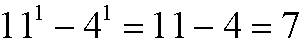
is divisible by 7.
Induction step: We assume that
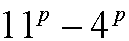
is divisible by 7, that is, that
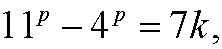
for some integer k. Then
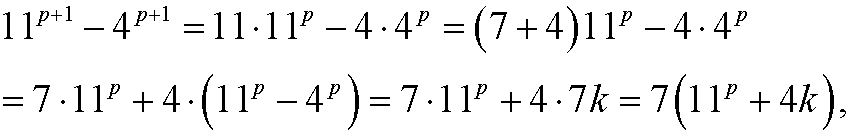
is also divisible by 7.
Since we have shown that the proposition holds for the basis step n=1 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=1,2,3,…
Example 4: Show that
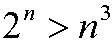
for n=10,11,12,…
Basis step:
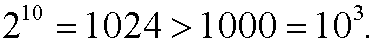
Induction step: Assume that the inequality holds for n=p, that is
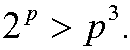
We want to show that it then also must hold for n=p+1, that is
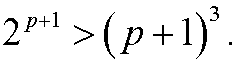
We have that
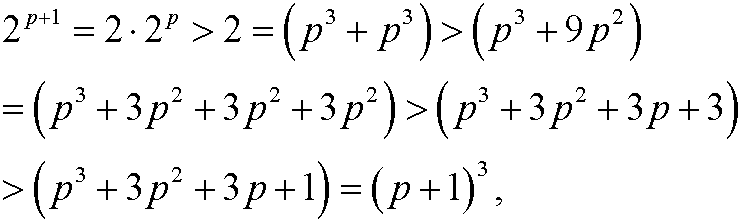
since p>9.
Since we have shown that the proposition holds for the basis step n=10 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=10,11,12,…
Example 5: Show that
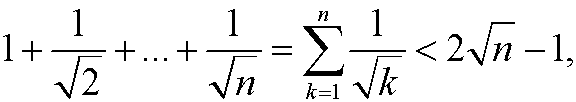
for n=2,3,4,…
Basis step:
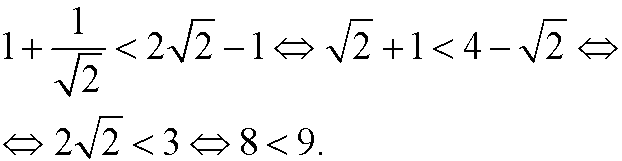
Induction step: Assume that the inequality holds for n=p, that is
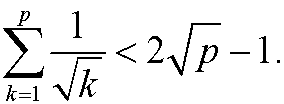
We want to show that it then also must hold for n=p+1, that is
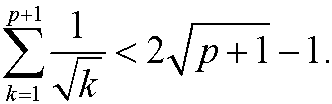
We have according to the induction assumption that
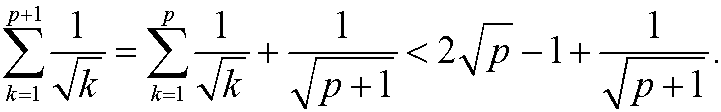
If we could have shown that
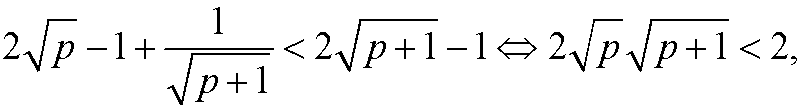
we would have been finished. However,
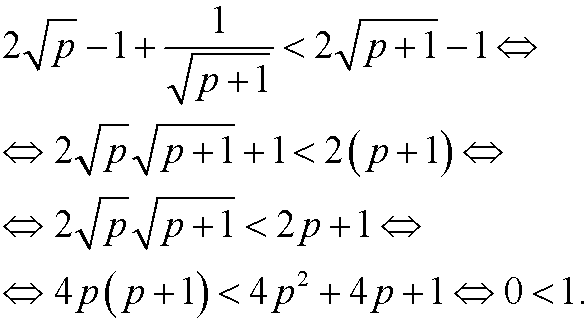
Since we have shown that the proposition holds for the basis step n=2 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=2,3,4,…
Example 6: Show that the recurrence equation
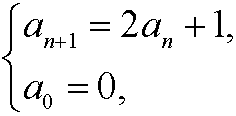
has the solution
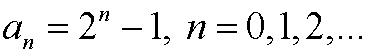
Basis step:
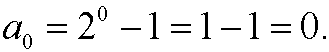
Induction step: Assume that the formula is correct for n=p, that is
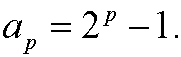
Then we have that
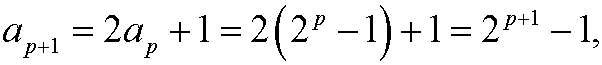
that is, the formula is correct also for n=p+1. Since we have shown that the proposition holds for the basis step n=0 as well as that the assumption that the proposition holds for n=p implies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=0,1,2,3,…
Example 7: Fibonacci‘s sequence {an}={1,1,2,3,5,8,13,21,…} is defined recursively by
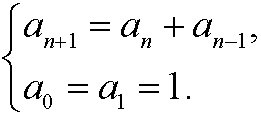
Show that the fibonacci numbers
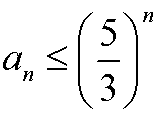
for n=1,2,3…
Basis step:
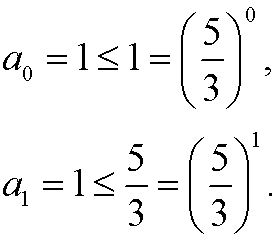
Induction step: Assume that the inequality holds for n=p and for n=p-1, that is
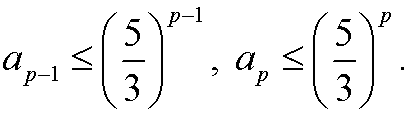
We want to show that it also must hold for n=p+1, that is
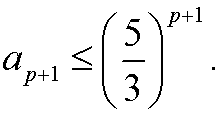
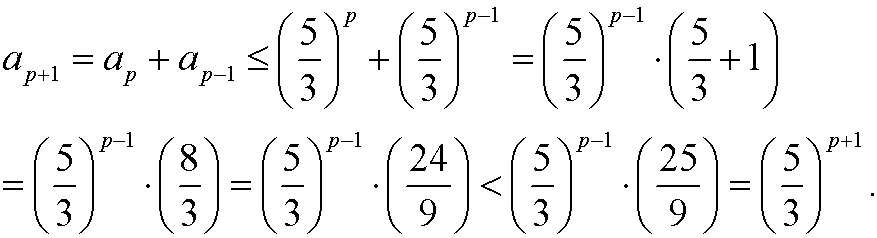
Since we have shown that the proposition holds for the basis step n=0,n=1as well as that the assumption that the proposition holds for n=p-1 and n=pimplies that it also holds for n=p+1, it follows from the principle of induction that the proposition is true for all integers n=1,2,3,…