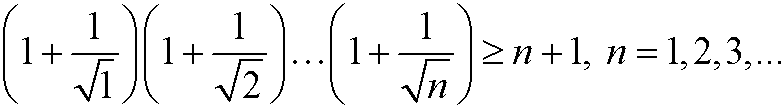1) Let A, B and C be sets. Show that
a)
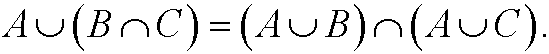
b)
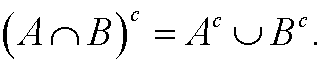
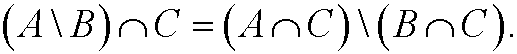
d)
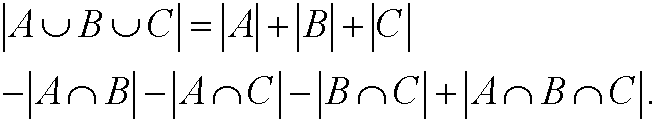
2) Express in decimal form
a) the binary number 1100011001.
b) the octal number 52701.
c) the hexadecimal number F20A9.
d) the number 6023 given in base 7.
3) Write the decimal number 7314
a) in binary form.
b) in octal form.
c) in hexadecimal form.
d) in base 5.
4) Write gcd(a,b) as all possible linear combinations of a and b when
a) a=95, b=46.
b) a=4171, b=1032.
5) Solve the diophantine equation
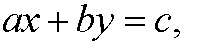
when
a) a=187, b=287, c=23.
b) a=187, b=286, c=23.
c) a=187, b=286, c=22.
6) Find the inverse to
a) 7 modulo 59.
b) 42 modulo 123.
7) Solve the equation
a)
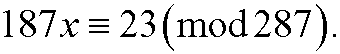
b)
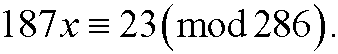
c)
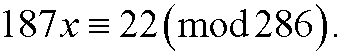
8) Prove by using induction that
a)
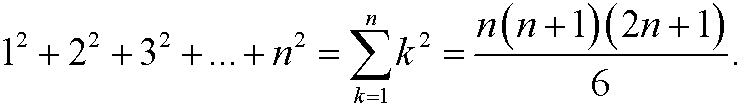
b)
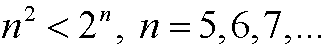
c) 42n-1 is divisible by 15 for n=1,2,3,…
d) the recurrence equation
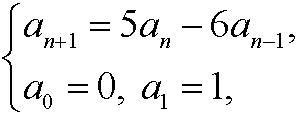
has the solution
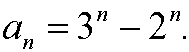
e) the numbers an in fibonacci’s sequence fulfills
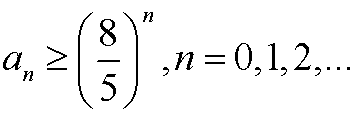
f)